- Při druhém výlovu je označená 1/16 vylovených ryb (5/80 = 1/16). Za předpokladu, že se ryby v rybníce rozdělili rovnoměrně, je tam 60 * 16 = 960 ryb.
-
Z podmínky je známo, že 40. pokolení, které nehyne po rozdělení, vyplní objem 1 m3 . K naplnění 2 m3 je třeba dvojnásobné množství. Zdvojnásobením tohoto
množství dostaneme množství 22 m3 , další zdvojnásobením 23 m3 atd. Množství 103 m3 (103 = 1000, 210 = 1024), takže 1027 m3 odpovídá přibližně 290 m3. To znamená,
že čtyřicáté pokolení musí překonat ještě 90 dělení, aby mělo objem jako Slunce. Celkový počet pokolení počítaje od prvého je 40 + 90 = 130, k čemuž
je potřeba 130 * 27 hodin, čili přibližně 146 dní.
-
a) Za uvedených předpokladů sní člověk za 60 let svého života přibližně 4,5 tuny masa. Porovnáme-li to s váhou býka (asi 0,5 tuny), potom by člověk mohl tvrdit, že snědl za 60 let 9 býků.
b) Za uvedených předpokladů vypije člověk přibližně 40 000 l tekutin. Porovnáme-li to s objemem vědra, které má asi 12 l, může člověk za 60 let života tvrdit, že vypil asi 3 500 věder tekutin.
-
Oba autobusy mají ujet stejně dlouhou dráhu, mají i tutéž hodinovou rychlost. Za 10 minut ujede jeden i druhý 16,875 km (135/80 * 10).
Vyjede-li autobus z města A, ujede cestu do C za týž čas jako autobus z města B k C 60 km. Autobusu z B zůstává do města C ještě 15 km. První je však již v městě C, kde čeká 10 minut. Druhý je vzdálen od C 15 km a tuto cestu ujede dříve než za 10 minut (má rychlost 16,875 km/10 3in).
Setkají se v městě C.
-
Vynásobíme-li 28/5 * 28/5 * 28/5, dostaneme asi 175. Jedno pštrosí vejce se rovná téměř dvěma stům slepičích. Jedním takovým vejcem by se mohlo nasytit téměř 100 lidí. Vejce váží přibližně 8-9 kg.
-
Umocněním první rovnice dostaneme x2 + 2xy + y2 = 4. Z druhé rovnice vypočteme 4xy = 4z2 + 4 a odečtením od předchozí dostaneme x2 - 2xy + y2 = -4z2 , tj. (x - y)2 = - 4z2 .
Tato rovnice může mít reálná řešení jen pro z = 0. Pak x - y = 0 a x + y = 2, z čehož vyplívá x = 1, y = 1, z = 0. Dosazením zjistíme, že vypočtená čísla vyhovují daným rovnicím.
-
K řešení této úlohy je třeba použít starého známého Archimédova zákona. Výsledek uvádíme opět v librách, koruna obsahovala 14,77 liber zlata a 5,23 liber stříbra.
-
Nejtvrdší byla A, potom B, C a nejměkčí D.
-
Z plné devítilitrové nádoby odlijeme dvakrát po čtyřech litrech, zbývající litr přelijeme do čtyřlitrové nádoby. Znovu nabereme 9 litrů, odlijeme 3 litry k doplnění čtyřlitrové nádoby a zůstává nám 6 litrů.
-
086 h = 51,6 min = 3 096s;
3 096 s - 360 s (na stanicích) = 2736.
Potom průměrná rychlost je:
45 600 m : 2 376 = 16 2/3 m/s
-
Tato úloha vede k neurčité rovnici
(x + 5)x = 4y - 1
Pravá strana rovnice je pro každé y číslo liché, levá strana je však pro každé x číslo sudé. Úloha tedy nemůže mít řešení.
-
30 oštěpů, 8 disků.
-
Chybu jsem udělali, když jsme dělili výrazem a - b, protože a - b, za předpokladu a = b, se rovná nule.
Dělit nulou však nelze.
-
V obou případech jsou koberce stejně dlouhé.
-
Označme první hledané číslo písmenem x. Prostřední je (x + 1) a další (x + 2). O nich platí:
(x + 1)2 = x(x + 2) + 1
Odstraníme-li závorky, dostaneme
x2 + 2x + 1 = x2 + 2x +1
Sestavená rovnice je identitou, tj. platí pro libovolné x. To znamená, že požadovanou vlastnost mají každá za sebou jdoucí čísla.
-
Abychom vyřešili úlohu, musíme vyhledat taková čísla, která jsou součastně dělitelná čtyřiceti i padesáti. Jsou to čísla 200, 400, 600, 800, 1000 atd. Sloupy stojí proti sobě po 200, 400, 600, … metrech.
-
Nacházíme se v bodě A. Z budovy je možno vyjít dveřmi B. Plán postupu je na obrázku.
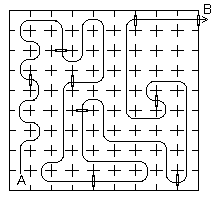
-
Z 90 lidí, kteří uměli německy, francouzsky, nebo německy i francouzsky, umělo 75 lidí německy. Tudíž 15 neovládalo tento jazyk. 7 osob neumělo francouzsky.
15 + 7 = 22,
90 - 22 = 68.
Dva jazyky ovládalo 68 lidí.
-
5 % dní nebylo chladno, 15 % dní nepršelo, 25 % dní nebylo zamračeno a 35 % dní bylo větrno. Sečteme-li tato procenta:
5 + 15 + 25 + 35 = 80 (%),
vidíme, že zůstává je 20 % dní, kdy bylo současně chladno, zamračeno, bezvětří a pršelo.
